Dr. Piccoli studies a number of fundamental problems in applied mathematics, including control of traffic via autonomous vehicles, mathematical modeling for systems biology, and measure differential equations. Below are highlights of his research accomplishments in these areas.
Control of traffic via autonomous vehicles
In recent years Dr. Piccoli addressed the problem of influencing vehicular traffic on road networks via the action of a small number of controlled autonomous vehicles (AV). The main results are:
- Ring-road experiments performed in July 2016 in Tucson, Arizona, showing reduction of up to 40% in energy consumption and 98% in breaking events using a single AV. The research was spotlighted in a number of venues, including ACM Tech News, NSF news, International Business Times, Engadget, The Drive, MIT Technology Review, Smithsonian Magazine and others.
- The research involved multiple universities (University of Arizona, UC Berkeley, University of Pennsylvania, Temple University, Vanderbilt University) and was funded via two NSF CPS projects (2015-17 with 1M$ and 2019-21 with 1.4M$) and recently by DoE (2020-22 with 3.5M$).
- Results were published in multiple papers including in top transportation journals such as Transportation Research Part C, Transportation Research Part D, and other journals such as SIAM Journal on Applied Mathematics and proceedings papers.
Figure 1. Experiments on a ring-road in Arizona.
Mathematical modeling for systems biology
The activity followed multiple lines of research with the following main results:
- A collaboration with the Sanofi, a major pharmaceutical company, focused on cholesterol metabolism and gave rise to joint published papers and team-taught graduate course at Rutgers–Camden, with final projects presented at the Sanofi’s U.S. headquarters. Sanofi sponsored two PhD student (Sean McQuade and Nathaniel Merrill).
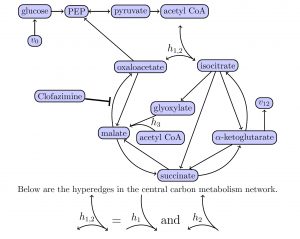
- We established a collaboration with the Gates Medical Research Institute on fighting tuberculosis. The Gates MRI was established in 2018 with the headquarter in Boston as an operating branch of the Bill and Melinda Gates Foundation. The collaboration focuses on advanced mathematical methods for metabolic and gene regulatory networks with main aim of optimizing the drug combinations to cure tuberculosis. The current state of the art in term of drug regimen include 4-drug therapies. Based on microarray data from NIH studies we created a first ranking of therapies to optimize effect (response curve on bacteria population) and received a lot of attention and interest. Preliminary results were already presented at a recent meeting in Nutty, NJ, organized by the Gates MRI.
- To deal with bio-chemical networks we defined new mathematical objects called ubergraphs, which generalize the concept of graph. Moreover, we developed the first tools to apply ubergraphs to dynamics of bio-chemical networks, including network flow results.
- We collaborated on various other projects with the Center for Computational and Integrative Biology, including on Developmental Biology with Nir Yakoby, on Circadian Rhythms with Kwnagwon Lee, on Forensic Science with Catherine Grgicak and others.
Figure 2. Example of ubergraph for the central carbon metabolism of Mycobacterium Tuberculosis.
Measure differential equations
Recently we provided new theory of differential equations for measures (called Measure Differential Equations). The first paper was published on Archive for Rational Mechanics and Analysis, one of the top-notch journal for mathematical modeling and analysis. The theory was presented at multiple venues, including Scuola Normale Superiore of Pisa, Pennsylvania State University, at a colloquium at University of California at Berkeley, and at the IEEE Conference on Decision and Control and American Control Conference. There is a wide and increasing interest for the theory.
Figure 3. Members of Piccoli’s lab with Joseph Lopez in Fall 2019. Left to right: Sydney Truong, Nathaniel Merrill, Sean McQuade, Joseph Lopez, Benedetto Piccoli, Zheming An, Amaury Hayat and Xiaoqian Gong.